Denoising
During acquisition and transmission, images are often corrupted by additive noise. The aim of a denoising algorithm
is to reduce the noise level, while preserving the image features. There is a big diversity of estimators used as denoising
systems. One may classify these systems into two categories: those directly applied to the signal and those who use a WT before
processing. In fact, Donoho and Johnstone introduced the word denoising in association with the wavelet theory
(http://www-stat.stanford.edu/~donoho). The multiresolution analysis performed by the WT has been shown to be a powerful tool
to achieve good denoising. In the wavelet domain, the noise is uniformly spread throughout the coefficients, while most
of the useful information is concentrated in the few largest ones (sparsity of the wavelet representation). The corresponding
denoising methods consist of three steps:
1) the computation of the forward WT;
2) the filtering of the wavelet coefficients; and
3) the computation of the IWT of the result obtained.
Consequently, there are two tools to be chosen: the WT and the filter. In what concerns the first choice, we currently
use a new implementation of the Hyperanalytic Wavelet Transform (HWT). Concerning the second choice, numerous nonlinear
filter types can be used in the WT domain. A possible classification is based on the nature of the noise-free component of
the signal to be processed. Basically, there are two categories of filters: those built assuming only the knowledge of
noise statistics (a nonparametric approach) and those based on the knowledge of both signal and noise statistics (a parametric
approach). For more information, see the The use of
wavelet theory for decision making project page, Director: Alexandru Isar, Members: Ioan Nafornita, Sorin Moga, Corina Nafornita, Maria Kovaci,
Marius Oltean, Ioana Firoiu.

The denoising is a pretreatment required for EKG processing (segmentation in this example).
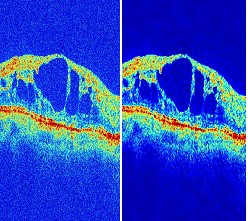
There are images (SAR, SONAR, biomedical) perturbed by speckle noise (left). The result of a denoising procedure is
presented in the right image.
Selected Publications:
- Alexandru Isar, Dorina Isar, Andre Quinquis,
"
Multi-Scale MAP Denoising of SAR and SAS Images",
Sea Technology,
INSTRUMENTATION: MEASUREMENT, PROCESSING & ANALYSIS, February 2007, Vol. 48, No. 2, pp.46-76
- A.M. Atto, D. Pastor, A. Isar, "
On the statistical decorrelation of the wavelet packet coefficients of a band-limited wide-sense stationary random process",
Signal Processing, Elsevier, vol. 87, Issue 10, October 2007, Pages 2320-2335, Special Section: Total Least Squares and
Errors-in-Variables Modeling, ISSN: 0165-1684;
- Alexandru Isar, Dorina Isar, Ioana Adam, "Denoising
Sonar Images", Proc. The Romanian Academy, Series A, Vol. 7, No. 2, May - August 2006, pp. 1-14,
ISSN: 1454-8267.
- Sorin Moga, Alexandru Isar, SONAR images despeckling using a Bayesian approach in the wavelet domain, Proc. SPIE Europe: Photonics Europe, Vol. 7000: Optical and Digital Image Processing, 700029 (Apr. 25, 2008), Strasbourg, France, ISBN: 97808194 71987 [pdf] [ppt]
- Ioana Adam, Corina Nafornita, Jean-Marc Boucher, Alexandru Isar, " A Bayesian Approach of Hyperanalytic Wavelet Transform Based Denoising", IEEE International Symposium on Intelligent Signal Processing, WISP 2007, Alcala de Henares, October 3-5, 07.
- Ioana Adam, Corina Nafornita, Jean-Marc Boucher, Alexandru Isar," A New Implementation of the Hyperanalytic Wavelet Transform", International Symposium on Signal, Circuits and Systems, ISSCS 2007, Iasi, Romania, 12-13 July 2007.
- Oltean M., Boucher J.-M., Isar A., "Filtering in the Diversity-Enhanced Wavelet Domain Applied to ECG Signals Denoising", Proceedings, 2006 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP 2006, Vol. 2, 14-19 May 2006 pp.II-1196 - II-1199, ISBN 1-4244-0469-X.
- A. Isar, S. Moga, I. Nafornita, J.-M. Augustin, R. Fablet, X. Lurton, D. Isar, " Adaptive Bivariate Shrinkage with Reduced Sensitivity", Proc. International Conference Communications 2006, Bucharest, June, 3-4, 2006, Round table under the aegis of the Romanian Academy of Technical Sciences, pp. 67-74,ISBN(10) 973-718-496-3, ISBN(13) 978-973-718-496-2.
- A. Isar, S. Moga, C. Nafornita, M. Oltean, I. Adam, "Image Denoising Using Wavelet Transforms With Enhanced Diversity", Proc. International Conference Communications 2006, Bucharest, June, 3-4, 2006, ISBN(10) 973-718-496-3, ISBN(13) 978-973-718-496-2, pp.161-164.
|

