Nonlinear techniques in telecommunications
The identification and compensation of unwanted nonlinearities are required in many
telecommunications systems in order to improve the system performances.
1. Volterra models
Nonlinearities representation is very important because the compensation technique depends on the model used.
The Volterra filter is widely used to model unwanted nonlinearities and provides also compensations techniques.
The major drawback of the Volterra technique is due to the computational complexity required to implement the model
and the compensation technique.
On the other hand, an efficient compensator requires accurate nonlinear system identification based on complex
Volterra estimators.
In practice, because the nonlinearities order is unknown, adaptive algorithms are suitable to estimate Volterra
kernels and to construct the nonlinear model.
Fast kernel estimation techniques are investigated in a large number of papers, in order
to construct higher order models that give accurate representations.
2. Neural networks equalizers
The multiple quadrature amplitude modulated (M-QAM) signals, more efficient in transmission from the
spectral point of view,
have known an expanding research interest. The M-QAM signals are severely affected by the nonlinear distortions,
because they have a variable envelope modulation. To compensate these unwanted distortions neural networks
equalizers for complex signals have been developed which are straightforward extensions from the real counterparts,
obtained by replacing the relevant parameters with complex values.
Recently, the RBF-NN have received considerable attention, since the MLP network is plagued by long training times
and may be trapped in bad local minima. The RBF-NN is able to approximate any arbitrary nonlinear function in the
complex multi-dimensional space with a reduced calculus complexity comparative to other NN. The RBF-NN often provides
a faster and more robust solution to the equalization problem than the MLP . In addition, the RBF-NN equalizer
has a structure similar to the optimal Bayesian symbol decision equalizer, so its performance is better than the
MLP equalizer performance.
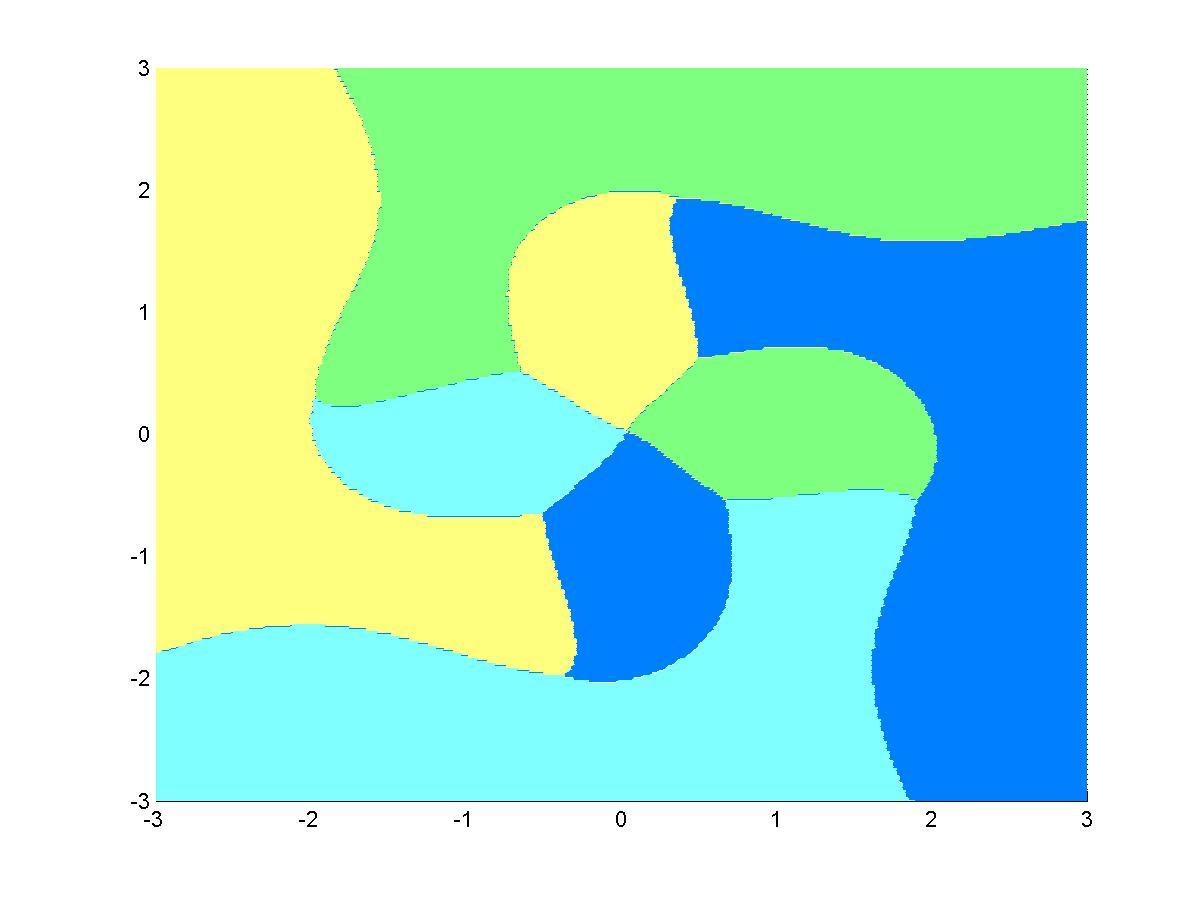
Decision regions of an RBF-NN complex equalizer in a complex data space,
which have strong nonlinear decisions boundaries
Selected Publications:
- Georgeta Budura, Corina Botoca, "
Efficient Implementation of the Third Order RLS Adaptive Volterra Filter",
Facta Universitatis, Nis, Serie Elec.Energ.,vol.19,no.1, April 2006, pp.133-141, ISSN 0353-3670
- Georgeta Budura, Corina Botoca, "
Practical considerations regarding the identification of a nonlinear system",
Revue roumaine des sciences techniques, serie Electrotechnique et energetique,
ISSN-0035-4066, Tome 51, 1, pp. 79-90, 2006
- Georgeta Budura, Corina Botoca, "
La construction d'un modele nonlineaire a l'aide de series Volterra et Wiener",
Revue roumaine des sciences techniques, serie Electrotechnique
et energetique, Tome 50, Vol. 4, pp. 465-475.
- Botoca Corina, Budura Georgeta, Neural,
"Symbol Decision Equalizer using Competitive Learning",
WSEAS Transactions On Circuits And Systems, Issue 6, Volume 5, June 2006, pp.829-836
- Botoca Corina, Georgeta Budura, Nicolae Miclau,
"Radial Basis Function equalization using
competitive learning", Revue Roumaine des Sciences Techniques, Serie Electrotechnique et
Energetique, Tome 50, Vol. 4, 2005 pp. 451-464.
|

